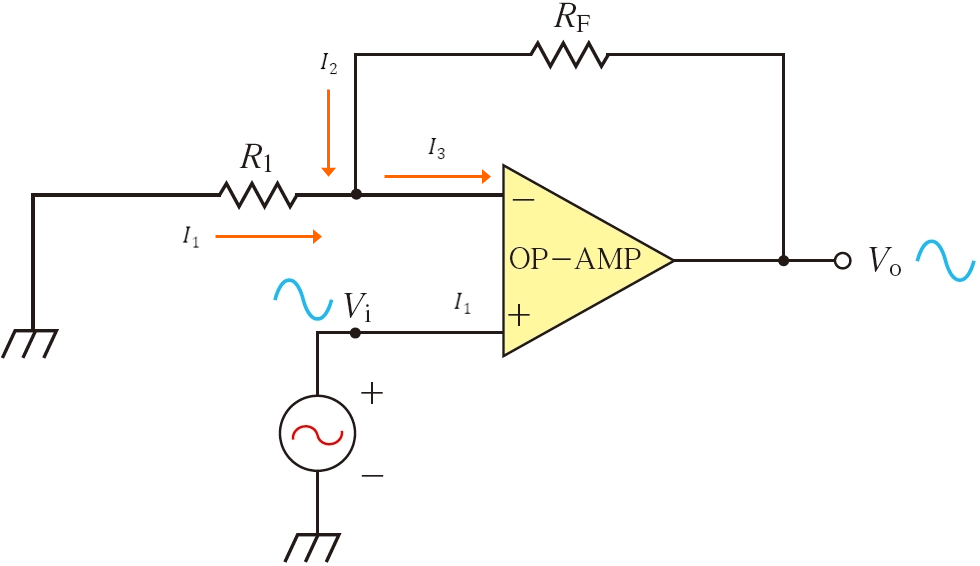
비반전 증폭 회로를 해석하기 위해 비반전 증폭 회로에서 다루었던 아래 두 개의 식을 다시 한 번 살펴본다.
$$V_{-} = V_{+}$$
$$i_{-} = i_{+} = 0$$
가상 단락에 의해 비반전 입력 단자와 반전 입력 단자의 전압 값은 같고, 연산증폭기의 입력 단자로 흐르는 전류는 0이기 때문에 반전 입력 단자에서 마디 해석을 위한 식을 세우면 다음과 같다.
$I_{1} + I_{2} = I_{3}$
각 전류를 전압과 저항으로 표현하면 $\frac{0 - V_{in}}{R_{1}} + \frac{V_{o} - V_{in}}{R_{f}} = 0$가 되고
이를 출력 전압에 대해 정리하면, $V_{o} = (1 + \frac{R_{f}}{R_{1}})V_{in}$이 된다.
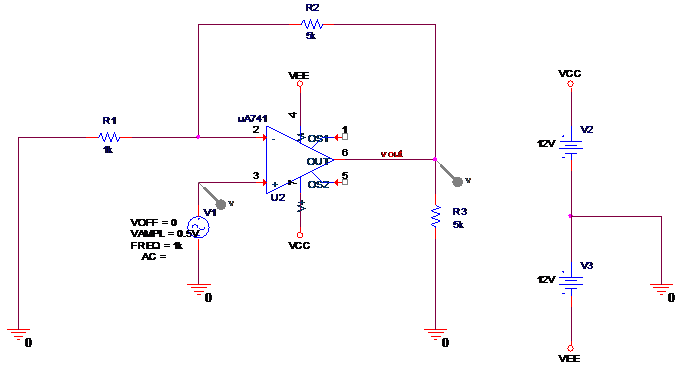
시뮬레이션을 위해 위와 같이 프로그램에서 회로를 구성하고 입출력을 관찰하면 다음과 같다.
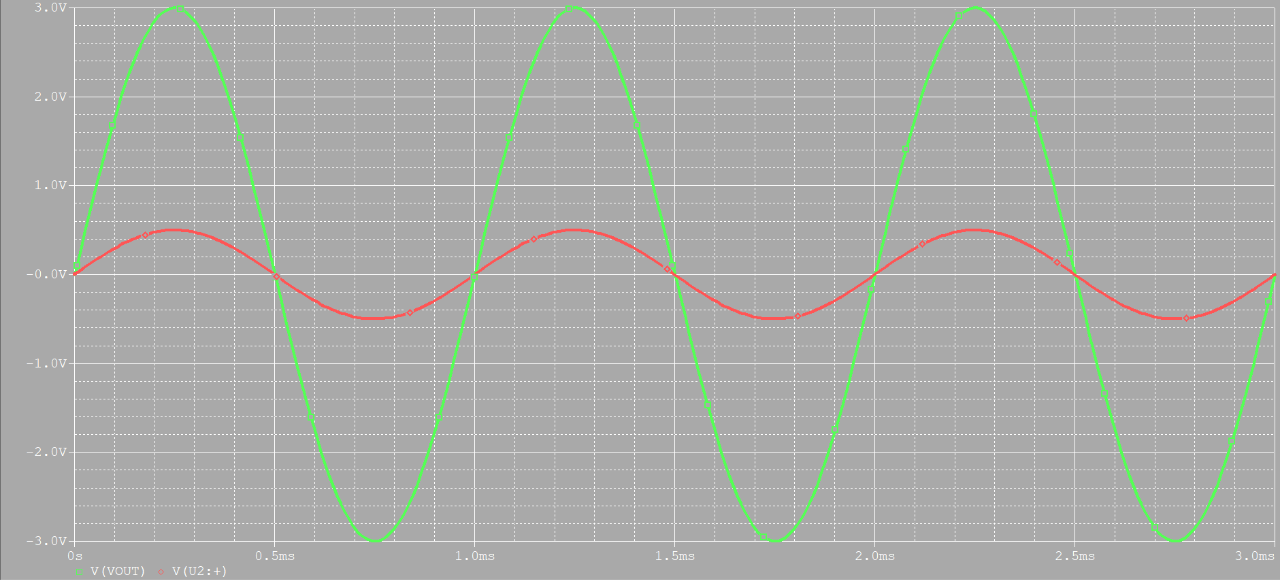
$V_{in} = 0.5sin\omega t$일 때, 출력을 예상해보면
$V_{o} = (1 + \frac{R_{2}}{R_{1}})V_{in} = 3sin\omega t$로
위와 같이 크기는 입력의 6배, 위상은 같은 파형이 출력된다.
고등학교 수업에서 사용하기 위해 정리한 내용입니다. 내용의 오류가 있다면 언제든 알려주세요.
또한 학습을 위해서라면 언제, 어디서든 활용하셔도 좋습니다.
'전기전자분야 > 전자회로 실험' 카테고리의 다른 글
| [전자회로 실험#13] 감산기 (0) | 2024.10.29 |
|---|---|
| [전자회로 실험#12] 가산기 (0) | 2024.10.29 |
| [전자회로 실험#10] 반전 증폭 회로 (0) | 2024.10.28 |
| [전자회로 실험#9] 연산증폭기 기초 (0) | 2024.10.21 |
| [전자회로 실험#8] 트랜지스터(BJT)의 동작점 Q 구하기_2 (0) | 2024.10.14 |



