연산증폭기를 응용한 회로 중 첫 번째로 알아볼 회로는 반전 증폭 회로다.
반전 증폭 회로를 알아보기 앞서 궤환(feedback)에 대해 먼저 알아본다. 궤환이라는 말 보다는 피드백이라고 생각하면 보다 이해하기 쉬울 것 같다. 회로에서 피드백이란 출력이 입력측으로 돌아와 영향을 미치도록 설계된 것을 의미하며 피드백 설계를 통해 안정도를 높히거나 발진회로를 설계하는 등 응용회로를 설계할 수 있다. 그래서 아래의 반전 증폭 회로는 출력에서 $R_{f}$를 통해 피드백을 거쳐 반전입력 단자로 들어오게 되는 피드백 경로가 구성되어있음을 확인할 수 있다.
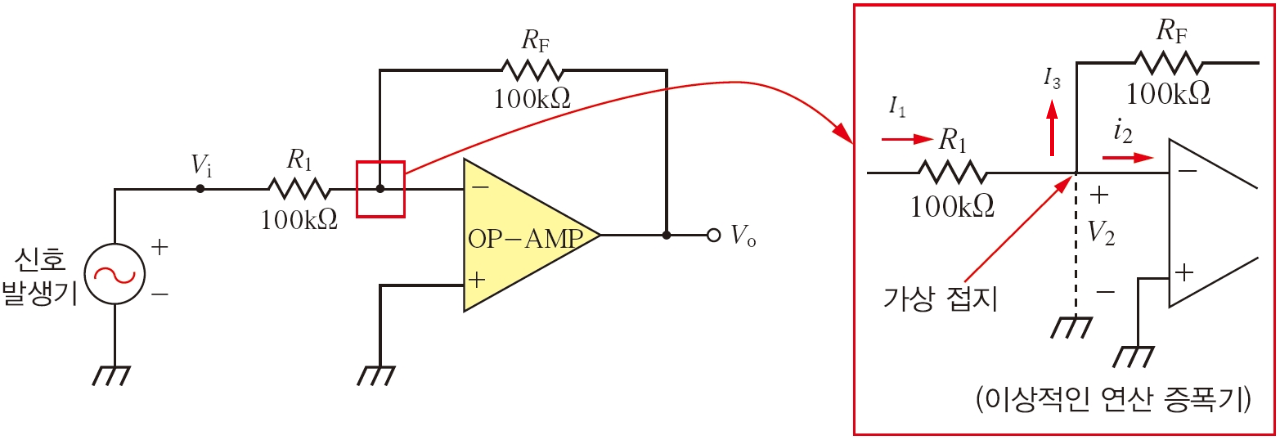
- 반전 입력 단자와 비반전 입력 단자는 가상 단락에 의해 같은 전위를 갖는다.
$$V_{-} = V_{+}$$
비반전 입력 단자와 반전 입력 단자는 실제로 연결되어있지는 않으나 단락되어있는 것처럼 같은 전압 값을 갖는다는 의미이다. 위의 그림에서는 비반전 입력 단자가 접지에 연결되어있으므로 가상 접지라는 표현을 사용하였으나 가상 단락이라는 더 포괄적인 단어로 표현할 예정이다.
- 연산증폭기 내부 저항($R_{in}$)은 $\infty $이므로 반전 입력 단자와 비반전 입력 단자로 연산증폭기 내부로 전류가 흐르지 않는다.
$$i_{-} = i_{+} = 0$$
이상적인 연산증폭기의 내부 저항 ($R_{in}$)은 무한대의 값을 갖기 때문에 전류가 흐를 수 없다. 실제 연산증폭기의 내부 저항은 무한대 값을 갖진 않지만 매우 큰 값을 갖기 때문에 흐르는 전류 또한 매우 작기 때문에 실제로도 전류가 흐르지 않는다고 가정한다.
연산증폭기 회로 해석을 위해 다음의 두 개의 위의 두 사항을 고려하여 반전 입력 단자에서 마디해석식을 세우면 다음과 같다.
$$I_{1} = I_{2} + I_{3}$$
$$\frac{V_{i} - 0}{R_{1}} = \frac{0 - V_{o}}{R_{f}} + 0$$
정리하면, $V_{o} = -\frac{R_{f}}{R_{1}}V_{i}$가 된다.
출력 전압 $V_{o}$는 입력 전압 $V_{i}$의 위상과는 반대로, 크기는 $R_{f} / R_{1}$의 비율에 따라 출력됨을 예상할 수 있다.
예상한 바와 같은지 확인하기 위해 다음과 같은 회로를 프로그램으로 구성한다.

$V_{in} = 0.5sin\omega t $ [V]
(시간에 따른 변화를 알아보기 위함이므로 입력 신호의 주파수와 관계된 부분을 간단히 $\omega$로 표현한다.)
출력 신호를 나타내는 식에 각 값을 대입하여 결과를 예상해보면
$V_{out} = -\frac{R_{2}}{R_{1}}V_{in} = -\frac{5k}{1k}0.5sin\omega t = -2.5sin\omega t$ [V]가 된다.
즉, 출력은 입력과 위상은 180도 다르고 크기는 5배인 정현파가 됨을 예상할 수 있다.
예상한 출력이 맞는지 확인을 위해 시뮬레이션 조건을 다음과 같이 설정한다.
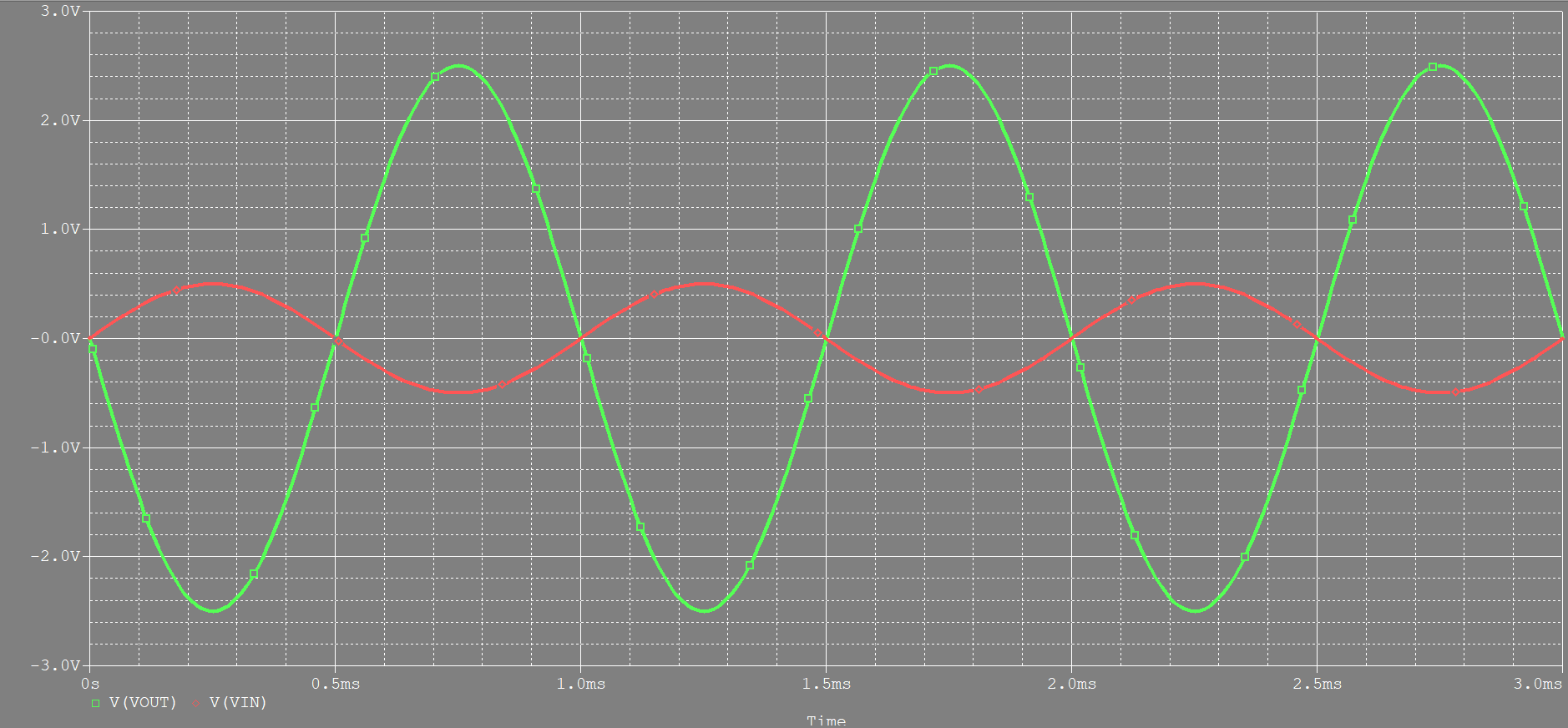
그리고 입력 신호와 출력 신호의 전압을 관찰하면 다음과 같이 초록색 출력은 붉은색 입력 신호에 크기는 5배, 위상은 반대가 됨을 확인할 수 있다.
'전기전자분야 > 전자회로 실험' 카테고리의 다른 글
| [전자회로 실험#12] 가산기 (0) | 2024.10.29 |
|---|---|
| [전자회로 실험#11] 비반전 증폭 회로 (0) | 2024.10.29 |
| [전자회로 실험#9] 연산증폭기 기초 (0) | 2024.10.21 |
| [전자회로 실험#8] 트랜지스터(BJT)의 동작점 Q 구하기_2 (0) | 2024.10.14 |
| [전자회로 실험#7] 트랜지스터(BJT)의 동작점 Q 구하기 (0) | 2024.09.24 |



